Strona domowa GDR!a

Matematyka wyższa w 10 minut

Wstęp

Kiedy byłem w technikum, zdarzało mi się czytać różne artykuły naukowe o wspaniałych algorytmach. Ze zrozumieniem koncepcji i matematyki nie miałem zazwyczaj problemów, ale kiedy przychodziło do przełożenia wzorów z całkami i pochodnymi na kod - zatrzymywałem się, gdyż była to bariera nie do przeskoczenia. Nie miałem dostatecznie dużo cierpliwości żeby znaleźć rozwiązanie w podręcznikach akademickich - owszem, próbowałem je czytać, ale jakoś nie znajdowałem nic co naprowadzałoby mnie na zamianę wzoru w kod.

Gdzieś w trakcie studiów udało mi się nabyć tą wiedzę, ale ponieważ szkoda stracić tyle lat na poznanie w gruncie rzeczy banalnych podstaw, postanowiłem opublikować to, czego się dowiedziałem. W postaci streszczonej, na ile się da - praktycznie i bez zbędnych dywagacji.

Pseudokod - w miarę możliwości - w języku C.

Sumy skończone

Wzór

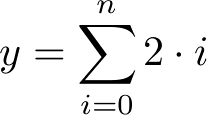
Wyjaśnienie

Wyrażenie pod znakiem sumy (sigmą) określa zmienną (i) która będzie się zmieniała oraz jej stan początkowy (0). Liczba nad sigmą określa maksymalną wartość tej zmiennej (n). Wyrażenie dalej jest obliczane dla każdej wartości. Suma wartości tych wyrażeń jest przypisywana do y.

Kod

y = 0;

for(i = 0; i <= n; i++)
{
	y += 2*i;
}

Sumy nieskończone

Wzór

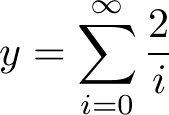
Wyjaśnienie

Jeśli wartość maksymalna to nieskończoność, i nie da się jej w jakiś sposób przekształcić - przy praktycznej implementacji po prostu sumuje się bardzo dużą ilość wartości wyrażeń.

Wartości poszczególnych wyrażeń prawie zawsze dążą wtedy do zera. Można założyć sobie zadaną dokładność (np. wynik ma być dokładny do +/- 0.2). Szukamy wtedy najmniejszego i dla którego wyrażenie sumowane jest mniejsze od tej dokładności (tutaj dla i=11, wyrażenie ma wartość 0.18).

Kod

y = 0;

for(i = 0; i <= 10; i++)
{
	y += 2/i;
}

Całki oznazczone

Wzór

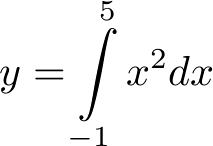
Wyjaśnienie

Całka oznaczona (czyli z cyframi nad i pod całką) jest podobna do sumy skończonej. Cyfra pod całką (-1) oznacza lewą granicę zakresu sumowania, nad całką (5) - prawą granicę. Za całką następuje wyrażenie sumowane (x²) zakończone dx. Litera następująca po d - w tym wypadku x - oznacza zmienną która będzie zwiększana w kolejnych iteracjach.

W naszym przypadku równoważna tej całce suma mogłaby być opisana wzorem .

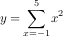Jest jednak różnica pomiędzy całką a sumą. W sumie zmienna zawsze zmienia się o 1, w całce - teoretycznie o nieskończenie małą wartość. W praktyce, wartość ta jest ustalana na dostatecznie małą aby zachować dokładność, ale przyzwoitość wymaga aby krok był co najmniej 10-100 razy mniejszy niż przedział całkowania. Zatem w naszym wypadku (-1..5) przybliżenie całki sumą skończoną jest za mało dokładne.

W kazdej iteracji, wartosc wyrazenia musi zostac dodatkowo przemnozona przez krok (dokladnosc).

Kod

krok = 0.01;
y = 0.0;

for(x = -1.0; x <= 5.0; x += krok)
{
	y += pow(x, 2) * krok;
}

/* Oczywiście, w kodzie niedydaktycznym używamy x*x zamiast funkcji pow() */

Różniczki (pochodne)

Wzór

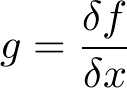
Wyjaśnienie

Funkcja g jest pochodną funkcji f po zmiennej x.

Sprawa wydaje się oczywista jeśli f jest określona wzorem - wtedy bierze się tablice matematyczne i po prostu szuka pochodnej. Co jednak zrobić w wypadku gdy funkcja f jest dana w postaci tablicy (jest np. linią obrazu)?

Pochodna (dokładnie mówiąc: iloraz różnicowy) jest wtedy tablicą różnic sąsiadujących elementów.

Kod

int f[10] = {12, 23, 34, 24, 32, 12, 21, 32, 56, 64};
int g[9];
int i;

for(i = 0; i < 9; i++)
{
	g[i] = f[i+1] - f[i];
}

Inne uwagi

• Pamiętaj o ograniczonej dokładności typów zmiennoprzecinkowych - przy wielu iteracjach potrafi pokazać rogi
• Tam, gdzie nie sprawia to problemu - najlepiej do zapisu liczb zmiennoprzecinkowych używac typu double
• Jeśli masz jakiś bardziej zaawansowany problem niż tu opisane - dział matematyki którym powinienneś się zainteresować to metody numeryczne, mój mail natomiast jest podany na górze strony.